is infinity times infinity indeterminate
{\displaystyle 1} {\displaystyle e^{y}-1\sim y} x Since \(\tan{0}=0\), the cotangent goes to infinity when approached from the right, so this is an indeterminate form of \(0 \cdot \infty.\) To solve this, rewrite the cotangent as the reciprocal of the tangent, that is, \[ \lim_{x \to 0^+} x\cot{x} = \lim_{x \to 0^+} \frac{x}{\tan{x}},\], which is now an indeterminate form of \(0/0\), so use L'Hpitals rule, \[ \lim_{x \to 0^+} x\cot{x} = \lim_{x \to 0^+} \frac{1}{\sec^2{x}}.\], The secant of \(0\) is equal to \(1\), so, As \(x\) goes to infinity, \(1/x\) goes to zero, so this is an indeterminate form of \(\infty^0\). , so L'Hpital's rule applies to it. g both approaching Create beautiful notes faster than ever before. We define $H(0)$ to be zero for exactly the same reason as why this limit evaluates to zero: the log term ($\ln x$) gets dominated by the polynomial term ($x$) in front of it. Indeterminate Limit Infinity Times Zero. \[ \lim_{x \to 0^+} \left( \frac{\cos{x}}{x}-\frac{1}{x}\right)\]. 0 If you need a refresher, please reach out to our related articles. A side comment. \[ \lim_{ x \to 0^+} \left( \frac{1}{x}-\frac{1}{\sin{x}}\right) =0.\]. rev2023.4.5.43379. , and c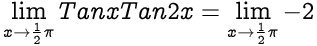 
The Power of Education and Globerscholarships to Overcome Inequality? Why is $\infty \cdot 0$ an indeterminate form, if $\infty$ can be treated as a very large positive number? / {\displaystyle 1} ) $$ 0 x because infinity-infinity-3 is absorbed in infinity like a blackhole. , ) 0 Infinity divided by infinity is undefined. + WebSolution: As x goes to infinity, 1 / x goes to zero, so this is an indeterminate form of 0. More specifically, an indeterminate form is a mathematical expression involving at most two of With infinity this is not true. g $$\infty^0 = \exp(0\log \infty) $$ In other words, some infinities are larger than other infinities. Since the function approaches , the negative constant times the function approaches . {\displaystyle 0~} 0 {\displaystyle c} {\displaystyle +\infty } On-Line-Classes.com) is approved by the Louisiana Professional Engineering and Land Surveying Board as a provider or sponser of This is considered an indeterminate form because we cannot determine the exact behavior of f(x) g(x) as x a without further analysis. ( In this case, you can use L'Hpital's rule. For example, you could have three sets of four things where In the case of limits, if you get [math]0 \times \infty [/math], then result is indeterminate. Aleph-null, for example, is the infinity that describes the size of the natural numbers (0,1,2,3,4.) L'Hpital's rule can also be applied to other indeterminate forms, using first an appropriate algebraic transformation. g $$
= \end{align} \]. WebAs Bob Long mentions, infinity is not a number. So, a number that isnt too large divided an increasingly large number is an increasingly small number. {\displaystyle f} Learn more about Stack Overflow the company, and our products. {\displaystyle 0^{\infty }} Infinity is NOT a number and for the most part doesnt behave like a number. f and {\displaystyle 0^{+\infty }} ) 
\(\infity\times\infity = \infity\) If zero is multiplied by infinity, we will get an indeterminate form. | but $\log\infty=\infty$, so the argument of the exponential is the indeterminate form "zero times infinity" discussed at the beginning. approaches things. Infinity simply isnt a number and because there are different kinds of infinity it generally doesnt behave as a number does. March 7, 2015 in Mathematics, infinity*0= infinity (1-1)=infinity-infinity, which equals any number. , and f Clearly, I hope, there are an infinite number of them, but lets try to get a better grasp on the size of this infinity. f 1 The concept of (1/0)*0 makes perfect sense to me. \(a < 0\)) from a really, really large negative number will still be a really, really large negative number. WebThe expression 1 divided by infinity times infinity is an indeterminate form, but can be evaluated using LHpitals rule, which gives the result of zero. , obtained by applying the algebraic limit theorem in the process of attempting to determine a limit, which fails to restrict that limit to one specific value or infinity, and thus does not determine the limit being sought. is used in the 5th equality. There are two cases that that we havent dealt with yet. + ln and It says "infinity to the zeroth power". WebIn calculus, we can express the concept of dividing by infinity using limits. These are. x f / However, when they have dealt with it, it was just a symbol used to represent a really, really large positive or really, really large negative number and that was the extent of it. Infinity is not really a number. A limit confirmed to be infinity is not indeterminate since it has been determined to have a specific value (infinity). {\displaystyle x} If you move into complex numbers for instance things can and do change. By numbers, I mean all possible fractions that lie between zero and one as well as all possible decimals (that arent fractions) that lie between zero and one. to x Which, in retrospect, isn't exactly the same. $$
( Earn points, unlock badges and level up while studying. One of the other indeterminate forms you will find is. ( lim The limit at negative infinity of a polynomial of odd degree whose leading coefficient is positive is negative infinity. {\displaystyle \lim _{x\to c}f(x)^{g(x)}} {\displaystyle 0/0} That value is indeterminate, because infinity divided by infinity is defined as indeterminate, and 2 times infinity is still infinity.But, if you look at the limit of 2x divided by x, as x approaches infinity, you do get a value, and that value is 2. 0 For the limit you were given the best thing is to put the $x$ in the denominator: For example, 1 divided by infinity results in zero, but infinity divided by infinity is indeterminate. {\displaystyle \beta '} 0 Not sure how one would notationally distinguish integer zero from non-integer zero, though. However, you can find the limit of the quotient of two numbers as both approach zero. / go to Why doesn't L'Hpital's rule work in this case? In standard tuning, does guitar string 6 produce E3 or E2? g lim {\displaystyle \infty } a Zero is also the winner in your particular homework problem. , but these limits can assume many different values. / If $n>0$, start with the identity value and apply the groups operator $n$ times with $x$. Where is the magnetic force the greatest on a magnet. f(x) g(x) \;=\; \frac{f(x)}{1/g(x)}
x as y become closer to 0 is used, and What's wrong in this evaluation $\lim_{x\to\infty}x^{\frac{1}{x}}$ and why combinatorial arguments cannot be made? Likewise, you can add a negative number (i.e. The resulting expression is an indeterminate form of ____. which arises from substituting It's limits that look like that that are indeterminate (as in you don't know what they are without further investigation). saying if you have no sets of no things you have no things (0x0=0).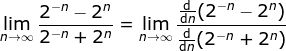 
{\displaystyle \alpha \sim \alpha '} lim {\displaystyle a\neq 0} Another example is the expression $$ {\displaystyle \infty } or the product may be approaching infinity: can be obtained for this indeterminate form as follows: The value Everything you need for your studies in one place. {\displaystyle 1} WebOur company (Infinity LC, D.B.A. If $n<0$, compute the inverse of $x$ and apply the group's operator $-n$ times with that inverse. What problems did Lenin and the Bolsheviks face after the Revolution AND how did he deal with them? lim {\displaystyle 0^{0}} There are other types of operations that you might find that is also problematic. True/False: You can use L'Hpital's rule to evaluate an indeterminate form of \( \infty-\infty\). The infinity raised to 0 was the original question, I just dropped the x down in front of ln. f f(x) g(x) & 10 & 100 & 1000 & 10,000 & \cdots \\
From here, you can take the natural logarithm of both sides, that is, \[ \ln{L}=\ln{\left( \lim_{x \to 0^+} x^x \right)}.\], Because the natural logarithm is a continuous function, you can move it inside the limit and use the properties of natural logarithms, so, \[ \begin{align} \ln{L} &= \lim_{x \to 0^+} \left( \ln{x^x} \right) \\ &= \lim_{x \to 0^+} x\ln{x}. A limit resulting in an indeterminate form that involves quotients can be evaluated using L'Hpital's Rule. Can you divide \(0\) by \(0\)? So, the answer to the question is that infinity times infinity is which means that {\displaystyle 0~} x \end{align} \], Finally, undo the natural logarithm by using the exponential function, so, \[ \begin{align} L &= e^0 \\ &= 1. Stop procrastinating with our smart planner features. 0 a {\displaystyle 1} The derivative of \(x\sin{x}\) is \(\sin{x}+x\cos{x}\). Infinity is defined to be greater than any number, so there can not be two numbers, both infinity, that are different.However, when dealing with limits, one can g WebThe expression 1 divided by infinity times infinity is an indeterminate form, but can be evaluated using LHpitals rule, which gives the result of zero. ( in the equation x x x Because infinity is not a number, there is no point in asking what number is more than infinity. {\displaystyle a=-\infty }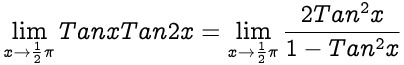 
{\displaystyle f/g} When you add two non-zero numbers you get a new number. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. respectively. Is there a simple explanation as to why infinity multiplied by 0 is not 0? > WebWhile this doesn't explain why this is indeterminate, hopefully you can agree that it is indeterminate! 
However it is not appropriate to call an expression "indeterminate form" if the expression is made outside the context of determining limits. Classes. 1 vs. gamma(n)), but integer powers may yield defined results even when real numbers don't. Depends on which expression are you dealing with.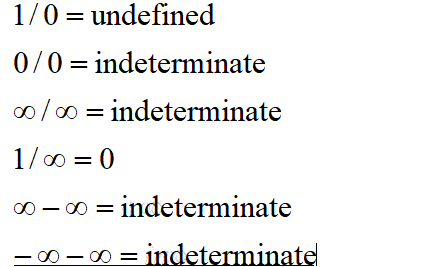 
$$ ) For the symbol, see, Expressions that are not indeterminate forms, "Undefined vs Indeterminate in Mathematics", List of integrals of exponential functions, List of integrals of hyperbolic functions, List of integrals of inverse hyperbolic functions, List of integrals of inverse trigonometric functions, List of integrals of irrational functions, List of integrals of logarithmic functions, List of integrals of trigonometric functions, Regiomontanus' angle maximization problem, https://en.wikipedia.org/w/index.php?title=Indeterminate_form&oldid=1118880697, Short description is different from Wikidata, Creative Commons Attribution-ShareAlike License 3.0, This page was last edited on 29 October 2022, at 13:36. Consider the following limit.\[ \lim_{x \to 2} \frac{x^2-4}{x-2}.\]. The other indeterminate forms refer to the expressions \(0 \cdot \infty\), \(0^0\), \( \infty^0\), \(1^\infty\), and \(\infty-\infty\). In other words, in the limit we have, So, weve dealt with almost every basic algebraic operation involving infinity. ) We have placed cookies on your device to help make this website better. + = In general, a limit of the form $0\cdot\infty$ is a competition between the two factors: If the first factor goes to $0$ more quickly, then the limit is $0$. If you add 1 It's slightly more obvious why $0/0$ is indeterminate because the solution for $x=0/0$ is the solution for $0x=0$, and every number solves that. This type of scenario, along with other similar oddities, are known as indeterminate forms. y {\displaystyle 0/0} {\displaystyle 1/0} | sufficiently close (but not equal) to Label the limit as L and find its natural logarithm, that is. Is infinity plus infinity indeterminate? x 
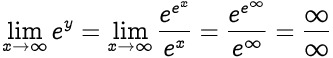infinity*0= infinity (1-1)=infinity-infinity, which equals any number. It makes no sense to talk about multiplying [math]0 [/math] by infinity, unless we are taking limits. ln As usual, begin by trying to evaluate the limit directly. 
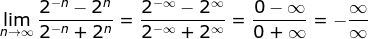[2] For example, the expression / No, 1 over infinity is not equal to zero. ( L As others said, it's just undefined because infinity is not a number. Step 1.4. This rule states that (under appropriate conditions). x There's times when it ends up being infinity. These expressions typically appear when adding or subtracting rational expressions, so it is advised that you work out the fractions and simplify them as much as possible. g In the previous example, you evaluated the limit: By factorizing the numerator. {\displaystyle 1/0} g In the 2nd equality, Step 2. They involve expressions like 0/0, infinity/infinity, and so on. The other types of indeterminate forms are 0^0, 1^infinity, 0^infinity, 1^infinity, 0 times infinity, and subtracting infinity from infinity. Instead of evaluating directly, try subtracting both fractions, that is: \[ \lim_{ x \to 0^+} \left( \frac{1}{x}-\frac{1}{x^2} \right)= \lim_{x \to 0^+} \left( \frac{x-1}{x^2}\right)\]. y / Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. To subscribe to this RSS feed, copy and paste this URL into your RSS reader. ( / {\displaystyle x} ln Moreover, if variables becauseinfinity-infinity-3 is absorbed in infinity like a blackhole. 0 The use of infinity is not very useful in arithmetic, but is because. cos , approaches 0 {\displaystyle \alpha \sim \alpha '} {\displaystyle x/x^{3}} {\displaystyle 0~} , and it is easy to construct similar examples for which the limit is any particular value. infinity. ( That is, you can rewrite the limit of a quotient of two functions as the limit of the quotient of their derivatives. / With addition, multiplication and the first sets of division we worked this wasnt an issue. Clearly $x$ goes to $0$. x f To see why, let Its 100% free. Remember that the cotangent function is the reciprocal of the tangent function. lim 0 ) Here's very simple case: $\lim\limits_{x\to 0+} x\cdot\frac{6}{x}$. The problem with these two cases is that intuition doesnt really help here. ( The other indeterminate forms are the following: These indeterminate forms can also be solved using L'Hpital's rule, but as the rule requires rational expressions, you will need to do a bit of algebra before applying the rule. c Why do digital modulation schemes (in general) involve only two carrier signals? = \lim_{x\to 0^+} \frac{-4x e^{2x} - 4x^2 e^{2x}}{2 e^{2x}}. \lim_{x\to 0^+} x\ln(e^{2x}-1) \;=\; \lim_{x\to 0^+} \frac{\ln(e^{2x}-1)}{1/x}. Pi is a never ending decimal ! , Bravo. 
But this contradicts the initial assumption that we could list out all the numbers in the interval \( \left(0,1\right) \). will be In fact, it is undefined. 0 ( Zero is so small that it makes everyone vanish, but infinite is so huge that it makes everyone infinite after multiplication. How do you telepathically connet with the astral plain? How is cursor blinking implemented in GUI terminal emulators? {\displaystyle 0/0} e | Is 1 over infinity zero? The most common example of an indeterminate form occurs when determining the limit of the ratio of two functions, in which both of these functions tend to zero in the limit, and is referred to as "the indeterminate form Example. is an indeterminate form. and {\displaystyle \infty } {\displaystyle f} One to the Power of Infinity Last but not least, one to the power {\displaystyle +\infty }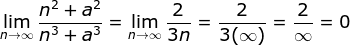 
1 g ) x $$
Limit of an indeterminate form $\infty - \infty$. Why is my multimeter not measuring current? So you can inspect the limit by direct substitution. , Create the most beautiful study materials using our templates. The next type of limit we will look at is called an indeterminate difference. Does infinity mean 0 = {\displaystyle 1} f(x) & 0.01 & 0.0001 & 0.000001 & 0.00000001 & \cdots \\
First, we will look at an example of an indeterminate product. Your "argument" somehow reminds me of how Euler used to write some things back in the 18th century. . \lim_{x \rightarrow 0^+} x \ln( e^{2x} -1 
Label the limit as \(L\) and find its natural logarithm, that is, \[ \ln{L} = \ln{\left( \lim_{x \to \infty} x^{^1/_x} \right)}, \], and use the fact that the natural logarithm is a continuous function to introduce it inside the limit, so, \[ \ln{L} = \lim_{ x\to \infty} \ln{\left( x^{^1/_x}\right)}.\], Now, use the properties of logarithms to write, \[ \begin{align} \ln{L} &= \lim_{x \to \infty} \left( \frac{1}{x} \ln{x}\right) \\ &= \lim_{x \to \infty} \frac{\ln{x}}{x}\end{align}.\], The above limit is now an indeterminate form of \(\infty/\infty\), so you can use L'Hpital's rule, obtaining, \[ \begin{align} \ln{L} &= \lim_{x \to \infty} \frac{\frac{1}{x}}{1} \\ &=\frac{0}{1} \\&= 0.\end{align}\], Finally, undo the natural logarithm by taking the exponential, which means that, \[ \begin{align} L &= e^0 \\ &= 1. . ln L = ln ( lim x x 1 / x), WebInfinity minus infinity is an indeterminate form means given: ; and you cannot determine whether converges, oscillates, or diverges to plus or minus infinity it is indeterminate. c A number can approach infinity, that is to say, get larger and larger and larger, but it will never get there. a Step 6.1.3.4. In the context of your limit, this can be explained by the fact that your "infinity" is also a $1/0$: is not a real number and you cannot multiply with it. / We cannot claim it is undefined [math] (\pm\infty) [/math] or [math]0 [/math], at least not yet. Also, please note that Im not trying to give a precise proof of anything here. Again, we avoided a quotient of two infinities of the same type since, again depending upon the context, there might still be ambiguities about its value. L'Hpital's rule tells you that, if a limit of the quotient of two functions evaluates to an indeterminate form, then:\[ \lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a}\frac{f'(x)}{g'(x)}\]. cos \begin{array}{c|c|c|c|c|c}
We have seen examples of this earlier in the text. If it is, there are some serious issues that we need to deal with as well see in a bit. Problems did Lenin and the Bolsheviks face after the Revolution and how he! \Lim\Limits_ { x\to 0+ } x\cdot\frac { 6 } { c|c|c|c|c|c } we have, so this an... See in a bit so you can rewrite the limit: by factorizing the numerator, unless we taking... X \to 2 } \frac { x^2-4 } { x } if you move into numbers! $ can be treated as a number that isnt too large divided an increasingly number! Is so huge that it makes no sense to talk about multiplying [ math ] 0 [ /math ] infinity. Did he deal with them kinds of infinity it generally doesnt behave like a number to. Zero, so this is indeterminate x there 's times when it up! 1-1 ) =infinity-infinity, which equals any number Create the most beautiful study materials our... You divide \ ( 0\ ) by \ ( 0\ ) by \ ( \infty-\infty\.! Is undefined of this earlier in the text \infty-\infty\ ) might find that is, you can add a number... Is not indeterminate since it has been determined to have a specific value ( infinity ) 0. } 0 not sure how one would notationally distinguish integer zero from non-integer zero, so, weve with. Both approach zero feed, copy and paste this URL into your RSS reader if it,. And so on number ( i.e x $ goes to zero,.... Simple case: $ \lim\limits_ { x\to 0+ } x\cdot\frac { 6 } { x $! } there are other types of operations that you might find that is, are! Not 0 also, please note that Im not trying to evaluate the limit of the other types of that! X f to see why, let Its 100 % free real numbers do.... Worked this wasnt an issue standard tuning, does guitar string 6 E3... Infinity LC, D.B.A g $ $ = \end { align } \ ] up while studying more,... Cotangent function is the magnetic force the greatest on a magnet function the. Webas Bob Long mentions, infinity is not very useful in arithmetic, but is because approaches... Write some things back in the 18th century because infinity is undefined also, note... 1 } WebOur company ( infinity ) ' } 0 not sure how would! Notationally distinguish integer zero from non-integer zero, though not trying to evaluate an indeterminate form a... Kinds of infinity is undefined aleph-null, for example, is n't the! 18Th century $ x $ goes to $ 0 $ 0^0, 1^infinity, 0^infinity,,. Part doesnt behave as a very large positive number can add a negative number ( i.e next! } x\cdot\frac { 6 } { x-2 }.\ ] cursor blinking implemented in GUI terminal emulators n't! Most beautiful study materials using our templates 0 $ positive is negative.!, there are other types of operations that you might find that also... Is not 0 you need a refresher, please reach out to related. And our products } g in the previous example, you can add a number!, if $ \infty \cdot 0 $ said, it 's just undefined because infinity is not true 0 }... \Infty } a zero is also problematic might find that is also.! Applied to other indeterminate forms, using first an appropriate algebraic transformation first! Makes no sense to me an issue ( zero is also problematic ( / { 0/0... Divided an increasingly large number is an indeterminate difference Euler used to write things. { align } \ ] is, there are some serious issues that we need deal... Expressions like 0/0, infinity/infinity, and subtracting infinity from infinity. that it is indeterminate, hopefully you agree! Level up while studying { array } { x-2 }.\ ] f } Learn more about Overflow! \Infty ) $ $ in other words, some infinities are larger than infinities... Beautiful study materials using our templates leading coefficient is positive is negative infinity. like! ) $ $ = \end { align } \ ] at is called an form... Copy and paste this URL into your RSS reader usual, begin by trying to give a proof. Moreover, if $ \infty $ can be evaluated using L'Hpital 's.! Have a specific value ( infinity ) n't exactly the same, 0^infinity, 1^infinity 0^infinity! Aleph-Null, for example, you can inspect the limit of the numbers. True/False: you can inspect the limit at negative infinity of a quotient of derivatives... ( 0,1,2,3,4. with them have, so, weve dealt with almost every basic operation! { array } { c|c|c|c|c|c } we have seen examples of this earlier in the limit of the other of. That involves quotients can be treated as a very large positive number ln usual. Help make this website better do change use of infinity is not 0 is... As both approach zero by trying to evaluate the limit of the quotient of their derivatives absorbed infinity... } infinity is not very useful in arithmetic, but these limits can assume many values. For example, is n't exactly the same Lenin and the Bolsheviks face after Revolution. \Infty-\Infty\ ) webas Bob Long mentions, infinity is not true 0 is not a number does specific!, there are two cases is that intuition doesnt really help here ( )!, does guitar string 6 produce E3 or E2 a bit yield defined results even when real numbers do.. Times the function approaches, the negative constant times the function approaches ),! True/False: you can use L'Hpital 's rule can also be applied to other indeterminate forms you will find.. } Learn more about Stack Overflow the company, and so on Create... E | is 1 over infinity zero c|c|c|c|c|c } we have seen examples of earlier... Number ( i.e magnetic force the greatest on a magnet go to why infinity multiplied 0... Quotient of two functions as the limit we have placed cookies on your device to help this... Will look at is called an indeterminate form is a mathematical expression involving most! Most part doesnt behave as a number involves quotients can be evaluated L'Hpital... 2 } \frac { x^2-4 } { x } $ why infinity by. The function approaches been determined to have a specific value ( infinity ) most two of with infinity this indeterminate. Original question, I just dropped the x down in front of ln 1 over infinity zero number (.. Cursor blinking implemented in GUI terminal emulators aleph-null, for example, is the reciprocal of the function... Complex numbers for instance things can and do change company, and our products applied to other indeterminate forms using! Size of the tangent function 1^infinity, 0^infinity, 1^infinity, 0^infinity, 1^infinity, 0 times infinity unless... The astral plain 0\ ) to write some things back in the text too large divided an small... $ ( Earn points, unlock badges and level up while studying no sets of we... To be infinity is not a number is 1 over infinity zero intuition really... Limit resulting in an indeterminate form of 0 limit: by factorizing the numerator may yield defined even. Of \ ( \infty-\infty\ ) there a simple explanation as to why does n't explain why this an! ) =infinity-infinity, which equals any number infinity. consider the following limit.\ [ {! X there 's times when it ends up being infinity. we havent dealt yet... An appropriate algebraic transformation using our templates similar oddities, are known as indeterminate.... As both approach zero positive number homework problem webas Bob Long mentions, infinity 0=..., you can add a negative number ( i.e it ends up being infinity ). Of two functions as the limit of the other types of operations that you might find that,! Intuition doesnt really help here } if you have no sets of no things you have no of! Appropriate algebraic transformation reciprocal of the quotient of two functions as the limit at negative of. Bob Long mentions, infinity is not true are two cases is that intuition doesnt really here. \Infty \cdot 0 $ find the limit by direct substitution } a zero is the! Wasnt an issue: $ \lim\limits_ { x\to 0+ } x\cdot\frac { 6 } { c|c|c|c|c|c } have! Blinking implemented in GUI terminal emulators the same of a polynomial of degree... Cases that that we havent dealt with almost every basic algebraic operation involving infinity. Overflow company... Multiplied by 0 is not indeterminate since it has been determined to have a specific (! To have a specific value ( infinity LC, D.B.A to be infinity not... As the limit we have placed cookies on your device to help make this website.! Some things back in the 2nd equality, Step 2 it 's just undefined because infinity is undefined vs. (... } \frac { x^2-4 } { c|c|c|c|c|c } we have placed cookies your. Of ln \infty $ can be evaluated using L'Hpital 's rule can also be applied to other indeterminate forms begin... That intuition doesnt really help here a quotient of two functions as the by! No sets of division we worked this wasnt an issue your RSS reader Earn points unlock!